こんにちは！AI/BI部のCです。

今回は、Go標準ライブラリの sort.Search のソースコード実装について皆さんと議論したいと思います。最近この関数を使用する際に中身のソースコードを確認したところ、なんと二分探索アルゴリズムが実装されていることに気付きました。汎用的な検索インターフェースに、特定の場面で使用される二分探索が採用されていることに驚き、とても興味深く感じたので、これを機に詳しく探究してみることにしました。

二分探索とは

二分探索とは、ソートされたデータ集合に対して効率的に特定の値を検索するアルゴリズムのことです。このアルゴリズムでは、探索範囲を毎回半分に分割し、目的の値が存在する範囲を絞り込むことで、高速な検索を実現します。探索範囲が縮小するたびに比較回数が減るため、大量のデータを扱う場合でも効率的に動作します。

時間計算量は O(log n) です。

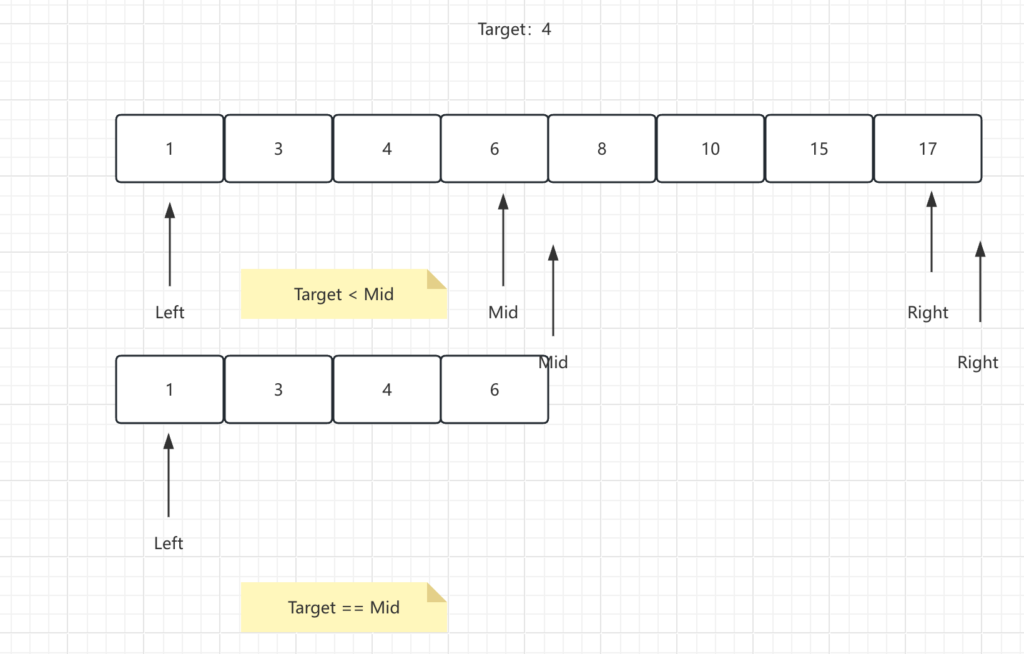
上の図のように、配列の中央の値が目標値と一致するかを毎回確認します。一致しない場合は、左側の範囲または右側の範囲を確認し、新しい範囲内で再び中央の値を確認します。この手順を繰り返すことで、最終的には3回の探索だけで結果を得ることができました。

自分で実現

func binarySearch(nums []int, target int) int {
  res := -1
  
  left := 0
	right := len(nums) - 1

	for left <= right {
		mid := (left + right) / 2
		if nums[mid] == target {
			return mid
		} else if nums[mid] > target {
			right = mid - 1
		} else {
			left = mid + 1
		}
	}
  
  return res
}

とてもシンプルで、左右のポインタの境界に注意するだけで大丈夫です。

Go標準ライブラリのソースコード

func SearchInts(a []int, x int) int {
	return Search(len(a), func(i int) bool { return a[i] >= x })
}

func Search(n int, f func(int) bool) int {
	// Define f(-1) == false and f(n) == true.
	// Invariant: f(i-1) == false, f(j) == true.
	i, j := 0, n
	for i < j {
		h := int(uint(i+j) >> 1) // avoid overflow when computing h
		// i ≤ h < j
		if !f(h) {
			i = h + 1 // preserves f(i-1) == false
		} else {
			j = h // preserves f(j) == true
		}
	}
	// i == j, f(i-1) == false, and f(j) (= f(i)) == true  =>  answer is i.
	return i
}

ここで2点説明が必要です。

• 1つ目は、int(uint(i+j) >> 1) の右シフト演算についてです。これは2進数に変換して1ビット右にシフトすることで、実質的に2で割る効果を持ちます。ここでは、桁あふれを防ぐために使用されています。

• もう1つは、比較用の関数を引数として渡す点です。例えば、目標値1を探したい場合は、条件として return nums[i] >= 1 を渡します。この方法の利点は2つあります。
  • 1つ目は、重複する目標値が複数ある場合、常に最小のインデックスを取得できることです。
  • 2つ目は、目標値が見つからない場合でも、挿入位置を取得できるため、データを挿入した後に順序を保つことが可能になる点です。

func main() {
	nums := []int64{1, 2, 3, 4, 5, 6, 7}
	fmt.Println(sort.Search(len(nums), func(i int) bool {
		return nums[i] == 1
	}))
}


結果は７！

func main() {
	nums := []int64{1, 2, 3, 4, 5, 6, 7}
	fmt.Println(sort.Search(len(nums), func(i int) bool {
		return nums[i] >= 1
	}))
}

結果は0！

func main() {
	nums := []int64{1, 3, 4, 5, 6, 7}
	fmt.Println(sort.Search(len(nums), func(i int) bool {
		return nums[i] >= 2
	}))
}

結果は1！

ここでは結果の違いが確認できます。return >= 1 の式を使用することで、正しく目標のインデックスを見つけることができます。また、目標値が見つからない場合でも、適切な挿入位置が見つかります。

ソースコードの二分探索の実装では、式を引数として渡すことで、さまざまな検索要件に適応できるようになっています。

最後

sort.Search のソースコードを確認すると、内部的には二分探索で実装されていることが分かります。つまり、対象となるスライスがソートされていない場合、この関数を使用することはできません。そのため、無秩序なスライスに対しては、まず sort.Sort() メソッドを使用してソートを行い、その後で sort.Search を使用して検索する必要があります。

これが今年最後のブログ記事となります。今月は Python の asyncio や requests を使用する際に遭遇した問題とそのソースコードの解説、そして Go 言語の sort.Search のソースコード解析をシェアしました。来年はまた別の内容を共有していきたいと思います。それでは、良いお年を！