おはようございます！AI/BI部のA.Kです。

眩くもやさしい初冬の日差しが届いてる心地よい晴れの続くこの頃、みんなお元気でお過ごしでしょうか

本日も、2024年のAI/BI部のAdvent Calendarとして、他のメンバーと同じく、1日1本の形で記事を投稿していこうと思っています。

どうぞ、よろしくお願いします！

構造化データの整合性問題

構造化データとは、ExcelやCSVファイルなど、行と列の概念を持つデータで、事前に定められた構造に整形されています。

企業の顧客データやアクセスのログデータなどが構造化データの主な例です。

一般的に、データベースで構造化データを管理しながら、SQL言語を使ってデータの検索や更新などの検索や集計、比較により、データの分析や活用をしています。

最近、AI技術の発展で、蓄積されたデータを活用していきたい気持ちを持つ人も多く増えました。過去の十数年のデータを薪のように、一気にAIモデルの学習に投入することが少なくないでしょう。

ただし、データの質により、AIモデルの学習が失敗することも多く、その場合、データ面の方にそもそもきちんと整合性が取れているかの疑問がよく浮かれています。

良いモデルを作るために、まずデータの質を保証しないといけないですが、数年分規模のデータの中、人力で多数のデータをチェックする方法以外、何か自動化できる手法で怪しそうなデータを特定するものがないかというような悩みを持っている方もきっといらっしゃるでしょう。

今回は構造化データを利用して、数値予測を目標としてAIモデルを作成したい場合、あやしいそうなレコードを事前特定して、効率を上げる手法を自分の経験上で紹介していきたいと思います。

PLS（部分的最小二乗）

PLS（部分的最小二乗）回帰は大学の統計学の授業、回帰分析の手法の１つとして紹介されたことがあるかもしれませんが、予測変数（Y）と観測可能な説明変数（X）との間の最大分散の超平面を探す代わりに、それらを新たな空間に射影することによって線形回帰モデルを探ることです。以下、PLS回帰に略称とさせていただきます。

予測変数（Y）が数値でなく、単なる分類である時は部分的最小二乗判別分析（PLS-DA）という派生法であるものになります。

PLS回帰の仕組みの話ですが、簡単に言うと、下の画像のようになります。予測変数（Y）と説明変数（X）の間で直接な線形回帰モデルを探すでなく、説明変数（X）の線形結合で潜在変数（T）を導出し、その潜在変数（T）の線形結合でさらに目的/予測変数（Y）を表現する形です。その中、予測変数（Y）ともっとも関連性強い潜在変数（T）とその線形結合による線形回帰モデルを見つけることになります。

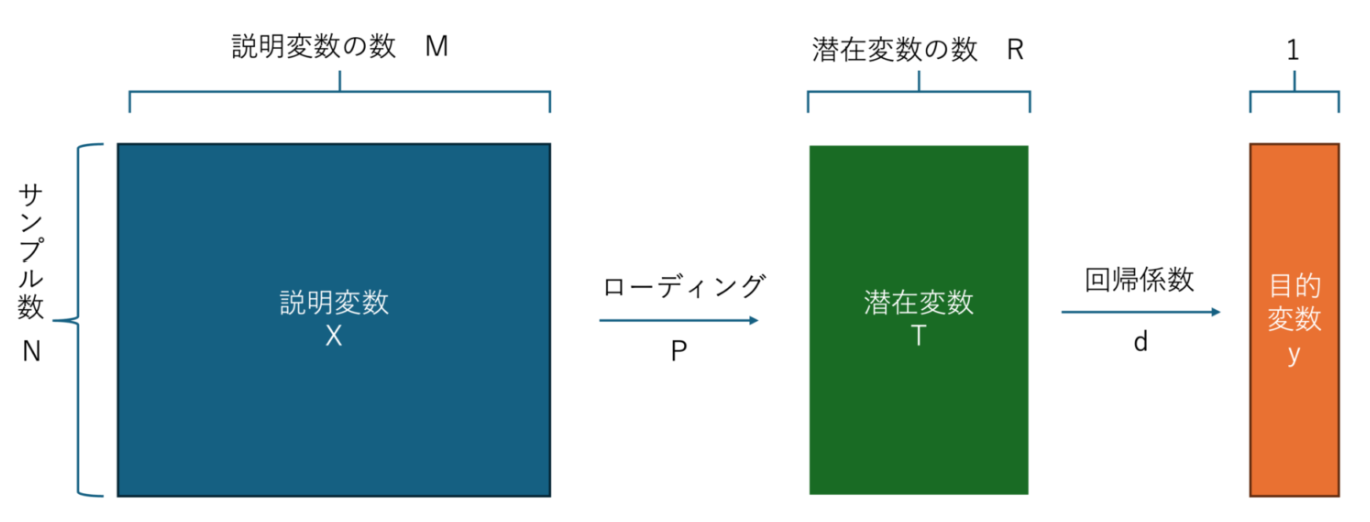
参考：【Python】部分的最小二乗回帰（PLS）を使ってみよう！

今日、PLS回帰は計量化学（ケモメトリクス）、感覚計量学などの関連領域において最も広く使われているそうです。

それでは、計量学によく使われている分析手法がAIモデルの学習に関わるデータセットの整合性と一体何か接点があるでしょう。早速、紹介していきましょう！

PLS回帰とAIモデル学習の関連性

構造化データのAIモデル学習と言えば、まず、もっとも一般的なNN深層学習モデルの仕組みを見ていきましょう。

下の画像のように、主に入力層、中間層、出力層の３段階の構造となります。

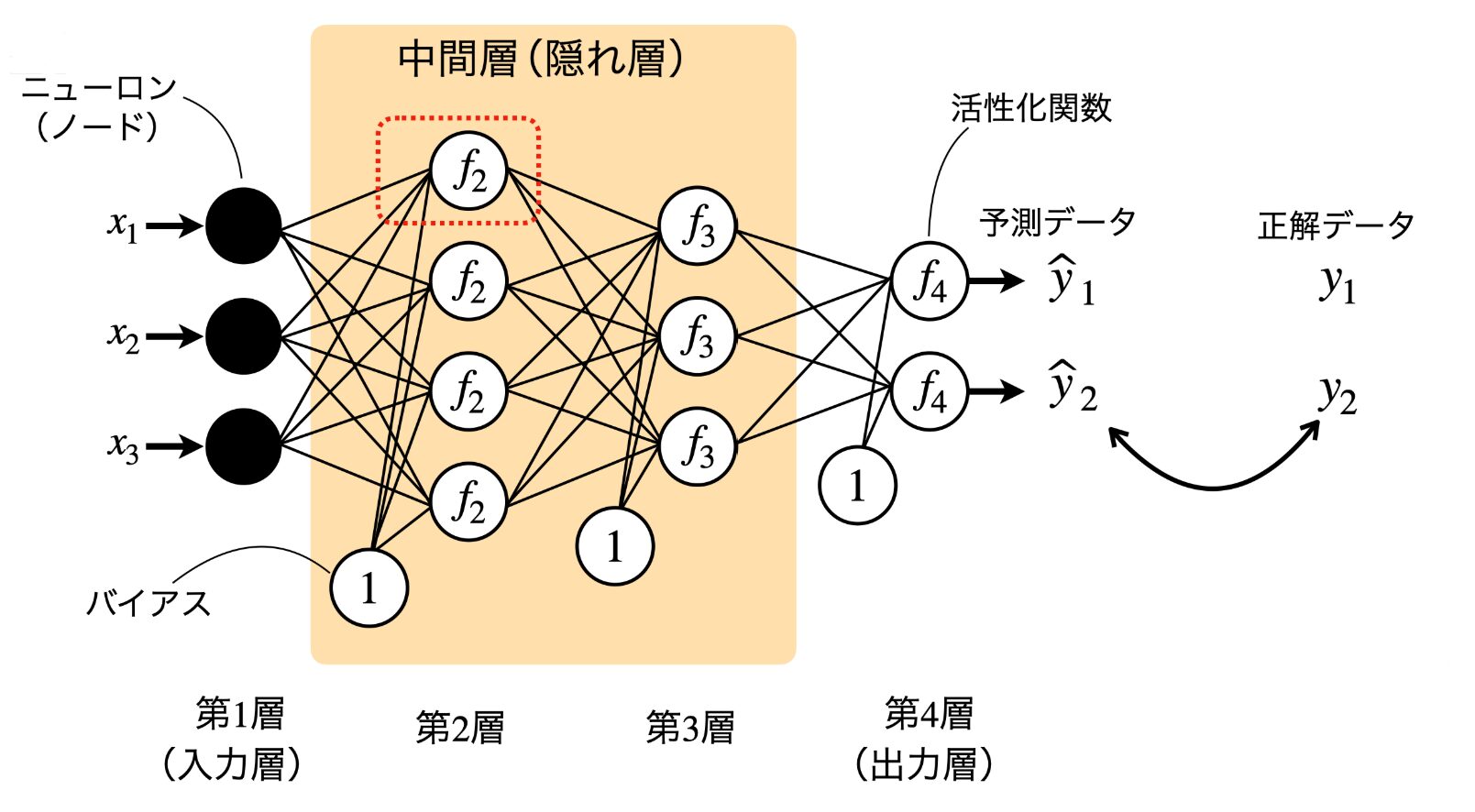
先程紹介したPLS回帰の仕組みと照合してみると、説明変数（X）に入力層、潜在変数（T）に隠れ層、予測/目的変数（Y）に出力層がそれぞれ相当することが分かるでしょう。

さらに、各層の結合方法を見ていくと、それぞれのノードの間にも線形結合の形で繋いでいることが気づけるではないか。なんとPLS回帰の上位バージョンのように見えますね！

構造自体に共通点が多いということはデータセットに対して、統計学の回帰分析手法で行った結果の傾向が深層学習ベースのAIモデル学習の参考材料として利用する価値が十分にあると考えます。

おわりに

今回は、構造化データの整合性問題およびPLSに関して簡単な紹介をさせていただきました。

整合性問題、AIモデル学習とPLSの関連性はざっくりどんなものなのかを分かっていただけたならうれしいです。

次回は、より具体的にPLSを利用して、整合性チェックを実施するかを掘り下げて紹介するため、実際のソースコードとグラフをを通して確認していきたいと思います！