Blog
ブログ

2024年12月15日

JPEGエンコーダーをつくろう(2) – SOHOBB AI/BI Advent Calendar 2024

はじめに

　こんにちは。この記事はSOHOBB AI/BI Advent Calendar 2024の15日目の記事となります。
私の担当記事においては、画像圧縮符号化における基礎的な技術についてPython実装を交えながら紹介する「JPEGエンコーダーをつくろう」シリーズの2本目の記事になります。

　前回は、JPEGエンコーダーにおけるクロマサブサンプリングについて以下のような内容をご紹介しました。

  • JPEGでは原画像から一部の情報を削ることで高い圧縮率を実現していること
  • クロマサブサンプリングでは色差情報を間引くことで情報量削減を行っていること
  • 情報量削減には人間の視覚特性に基づき劣化が目立たないよう工夫されていること

　今回はJPEGエンコーダーにおいてクロマサブサンプリングの後段の処理にあたるDCTと量子化についてご紹介したいと思います。

JPEGエンコーダーの処理の流れを示した図

DCTとは

　離散コサイン変換(DCT: Discrete Cosine Transform)とは、時間的/空間的に変化する離散的な信号を、振幅や周波数の異なるコサイン波の加重和での表現に変換する処理のことです。
DCTは、一般に有名なフーリエ変換の派生の一つですが、圧縮符号化の分野では主にDCT-Ⅱと呼ばれる方法が用いられることが多く、JPEGでもDCT-Ⅱを利用しています。
これは、DCT-Ⅱは一般に有名なフーリエ変換やサイン波を基底とするDSTと比較して、エネルギー圧縮の効率が高い(係数の大きさが偏る)ためです。
JPEGでは最終的にエントロピー符号を用いて符号化しているため、係数の偏りが大きいほど効率よく符号化できるのでうれしいのですが、これは次回の内容で取り扱おうと思います。

　さて、前回使用したクリスマスツリーのイラストを例に、DCTを実際に見てみましょう。
簡単のため、イラストはグレースケールに変換し64×64ピクセルにリサイズしてあります。
イラストのx=32の値(赤枠エリア)のみ抽出してみると、y軸に沿って輝度(Luminance)が変化する波としてとらえることができます。

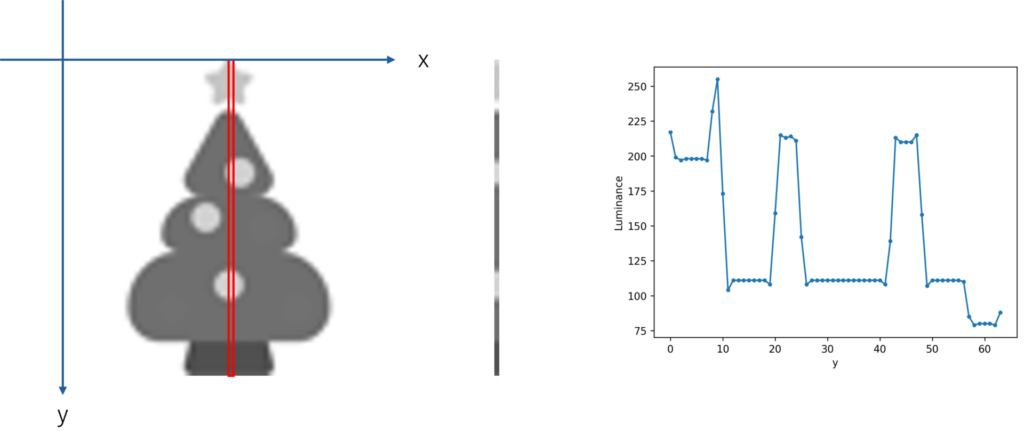
音声や画像といったデータは一般に、時間的/空間的な相関が高い傾向にあります。
イラストのようなベタ塗りが多い画像では特に顕著で、輝度の波形に平らな区間(隣のピクセルと同じ明るさ)が頻繁に出現することからもわかると思います。

　この波形を1次元のDCT-Ⅱを用いて周波数領域に変換すると、下記のような基底に対する64個の係数が得られます。

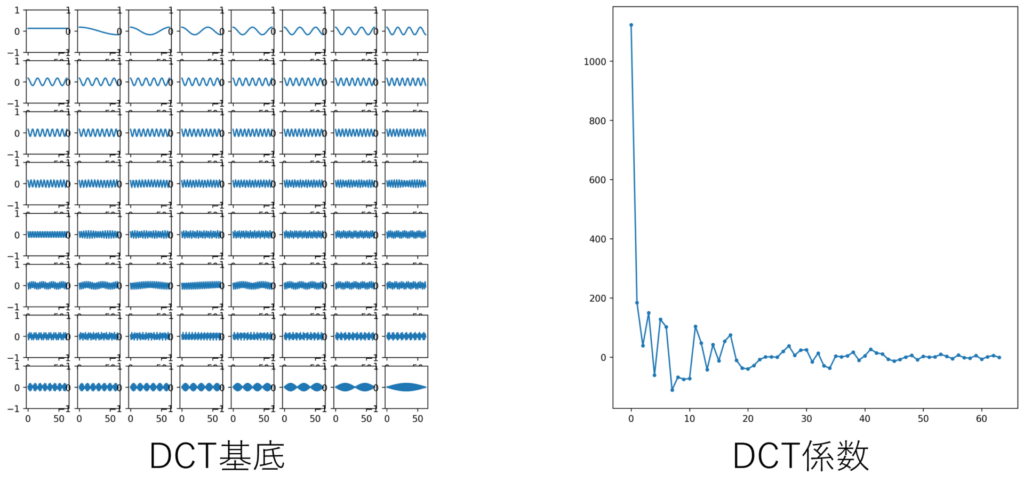
DCT基底はラスタスキャン順(左上隅から右へ、右端に到達したらひとつ下の行の左端から右端へ)並べて表示しています。左上隅の基底は常に一定であり変化しないためDC(直流)、その他の基底はAC(交流)と呼ばれていたりします。ACについては前半の基底ほど周波数が低く、後半の基底ほど周波数が高いことがわかります。
また、DCT係数を見てみると、係数の大きさが低周波成分に偏っていることがわかります。

　DCTはあくまでも時間/空間領域から周波数領域への変換なので、計算精度を無視すれば情報の損失はありません。元の信号を基底と係数に変換したわけですから、逆変換(加重和)を行うことで元の信号に戻すことができるはずです。
低周波成分から順に復元した結果がこちらです。

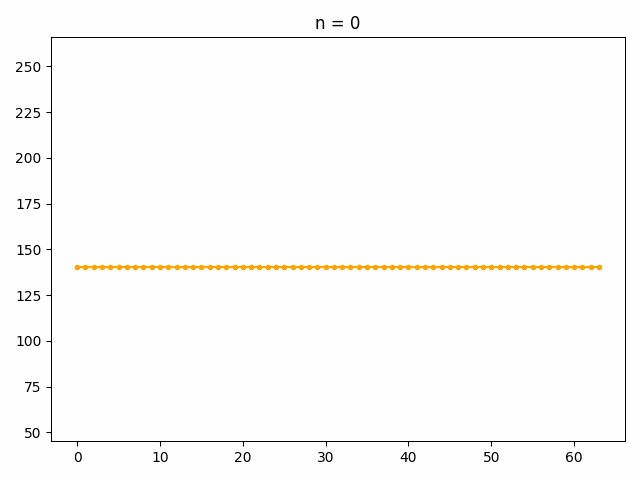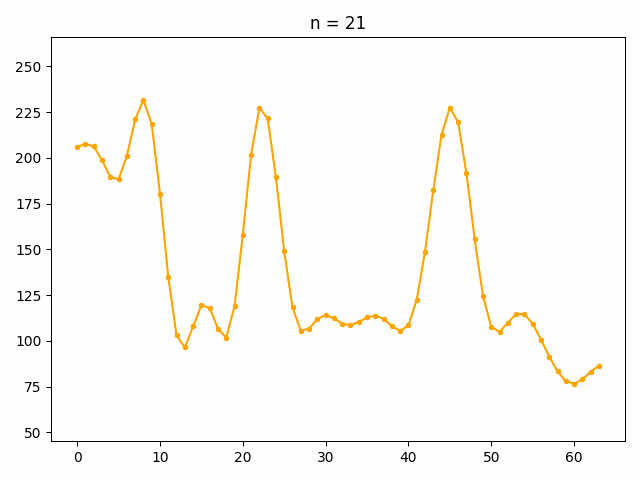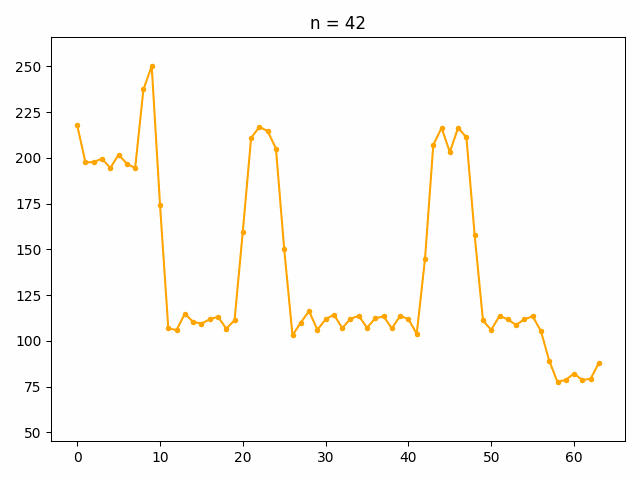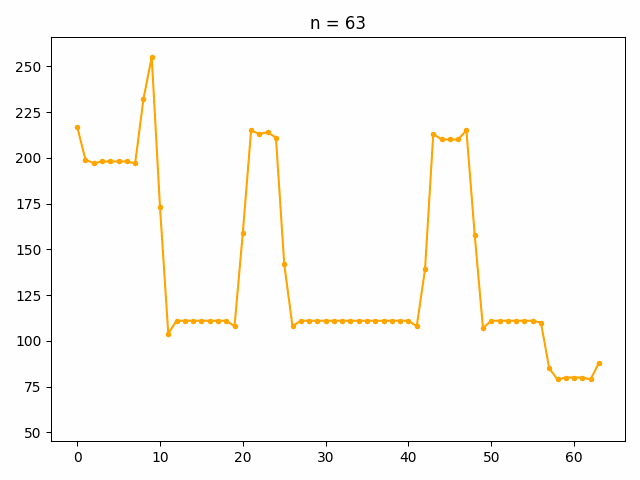
低周波数成分で元の信号の波形の全体的な性質を表現しており、波形の細かい部分については高周波成分で表現されていることがわかります。
最終的に復元された波形と元の波形を重ねてみると、変換の前後で情報の損失がないことがわかります。

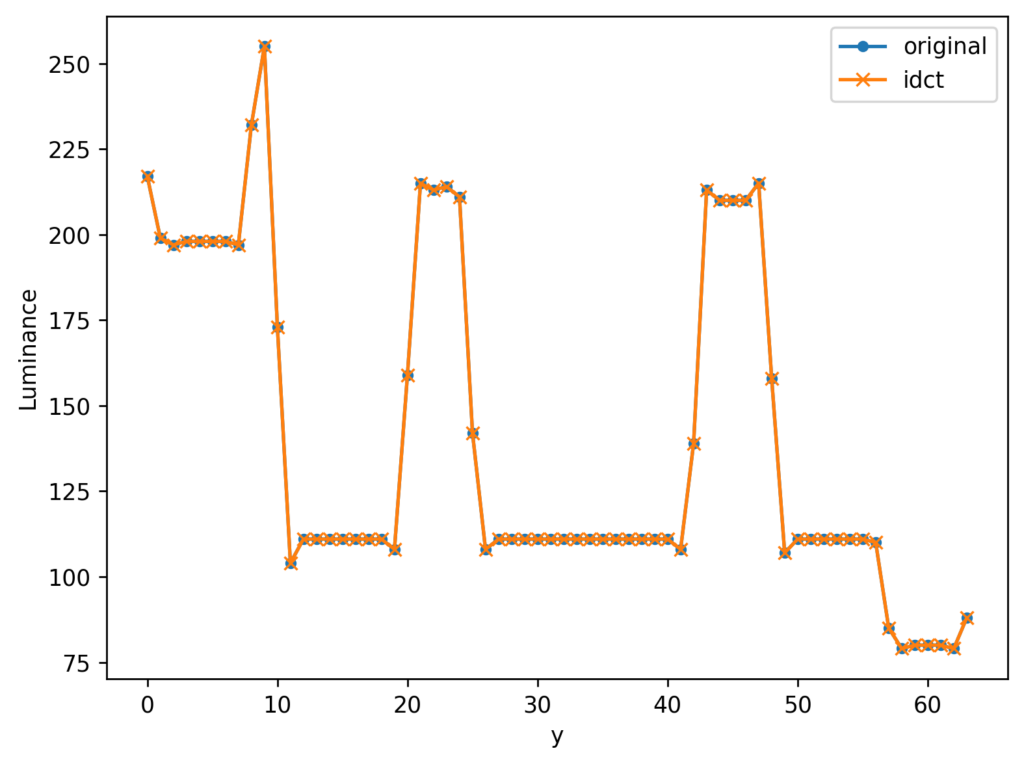
この例では、画像からy方向だけを取り出して1次元的にDCTを行いましたが、実際の画像はy方向に限らずx方向にも相関があるはずです。
実際のJPEGでは、クロマサブサンプリング後のYCbCr各成分を8×8ピクセルごとに分割し、2次元のDCTを適用しています。
2次元の場合でも考え方は同じで、8×8ブロックの画像をDCTすると8×8個の基底とその係数で表現されます。基底を可視化してみるとこのようになります。

次元が一つ増えたので画像のように表現していますが、1次元のときと同様に一定なDCと周波数の異なるAC基底の係数として表現される点は変わりません。

量子化

　さて、ここまでの内容で画像が空間的な相関・冗長性を持つこととDCTによってそれを取り除いた表現に変換できることがわかりました。
DCTそのものはあくまでも変換であり、情報量を直接削減することはありません。
JPEGでは、DCTによって得られた係数をより低精度な離散値で表すことによって情報量を削減しており、これを量子化と呼びます。

　量子化ではDCT係数を一定の幅の代表値で表すため、元の信号を毀損し劣化が生じます。もちろん、劣化はなるべく目立たせたくないため、ここでも人間の視覚特性を利用します。
JPEGの標準には含まれていませんが、広く利用されるlibjpeg-turboではDCT係数の量子化に以下の量子化テーブルを用いています。

C 
/* These are the sample quantization tables given in JPEG spec section K.1.
 * NOTE: chrominance DC value is changed from 17 to 16 for lossless support.
 * The spec says that the values given produce "good" quality,
 * and when divided by 2, "very good" quality.
 */
static const unsigned int std_luminance_quant_tbl[DCTSIZE2] = {
  16,  11,  10,  16,  24,  40,  51,  61,
  12,  12,  14,  19,  26,  58,  60,  55,
  14,  13,  16,  24,  40,  57,  69,  56,
  14,  17,  22,  29,  51,  87,  80,  62,
  18,  22,  37,  56,  68, 109, 103,  77,
  24,  35,  55,  64,  81, 104, 113,  92,
  49,  64,  78,  87, 103, 121, 120, 101,
  72,  92,  95,  98, 112, 100, 103,  99
};
static const unsigned int std_chrominance_quant_tbl[DCTSIZE2] = {
  16,  18,  24,  47,  99,  99,  99,  99,
  18,  21,  26,  66,  99,  99,  99,  99,
  24,  26,  56,  99,  99,  99,  99,  99,
  47,  66,  99,  99,  99,  99,  99,  99,
  99,  99,  99,  99,  99,  99,  99,  99,
  99,  99,  99,  99,  99,  99,  99,  99,
  99,  99,  99,  99,  99,  99,  99,  99,
  99,  99,  99,  99,  99,  99,  99,  99
};

量子化幅が輝度と色差信号で個別に用意されていることから、クロマサブサンプリングでも紹介した色の変化に鈍感な特性が利用されていることがわかります。
加えて、周波数成分ごとに異なる量子化幅が定義されており、高周波成分の量子化幅が低周波成分よりも大きい(粗く量子化されている)ことがわかります。

　JPEGにおいては、ブロックごとのDCT係数を量子化テーブルの値で除算し整数に丸めた値を符号化します。このため、量子化幅が大きく、DCT係数の小さい成分ほど歪みが大きくなり、劣化が生じる結果となります。

JPEGエンコーダーをつくろう(DCT & 量子化)

　さて、前回に引き続きPythonでJPEGエンコーダーをつくりましょう。
Pythonではscipyパッケージのfftモジュールに各種FFTが実装済みのため、これを利用します。
量子化については、ここではlibjpeg-truboの量子化テーブルを利用します。実際には、エンコーダーの実装者に委ねられているので、目的に応じてチューニングすることも可能です。
　また、画像の圧縮においては画質と圧縮率のトレードオフをとるために品質パラメータを指定できることが多いです。一般には、品質パラメータの値に応じて量子化テーブルをスケーリングすることで実現しています。

Python 
# NOTE: From libjpeg-turbo(https://github.com/libjpeg-turbo/ijg/blob/main/jcparam.c#L69)
LUMINANCE_QUANTIZE_TABLE = np.array(
    [
        [16, 11, 10, 16, 24, 40, 51, 61],
        [12, 12, 14, 19, 26, 58, 60, 55],
        [14, 13, 16, 24, 40, 57, 69, 56],
        [14, 17, 22, 29, 51, 87, 80, 62],
        [18, 22, 37, 56, 68, 109, 103, 77],
        [24, 35, 55, 64, 81, 104, 113, 92],
        [49, 64, 78, 87, 103, 121, 120, 101],
        [72, 92, 95, 98, 112, 100, 103, 99],
    ],
    dtype=np.uint8,
)
CHROMA_QUANTIZE_TABLE = np.array(
    [
        [16, 18, 24, 47, 99, 99, 99, 99],
        [18, 21, 26, 66, 99, 99, 99, 99],
        [24, 26, 56, 99, 99, 99, 99, 99],
        [47, 66, 99, 99, 99, 99, 99, 99],
        [99, 99, 99, 99, 99, 99, 99, 99],
        [99, 99, 99, 99, 99, 99, 99, 99],
        [99, 99, 99, 99, 99, 99, 99, 99],
        [99, 99, 99, 99, 99, 99, 99, 99],
    ],
    dtype=np.uint8,
)

def dct(plane: npt.NDArray[np.uint8], block_size: int = 8):
    """8x8ブロックに分割してDCT

    Args:
        array (npt.NDArray[np.uint8]): 入力のYまたはCbまたはCr成分
        block_size (int, optional): ブロックサイズ. Defaults to 8.

    Returns:
        npt.NDArray[np.float64]: DCT係数
    """
    plane = plane.squeeze()
    h, w = plane.shape
    pad_h = (block_size - (h % block_size)) % block_size
    pad_w = (block_size - (w % block_size)) % block_size

    # block_sizeの倍数になるようにパディング
    padded = np.pad(plane, ((0, pad_h), (0, pad_w)), mode="edge")

    # block_sizeに分割
    blocks = padded.reshape((h // block_size, block_size, w // block_size, block_size))
    blocks = np.einsum("rhcw->rchw", blocks)
    
    # ブロックごとにDCT
    coeffs = fft.dctn(blocks, type=2, axes=(-2, -1), norm="ortho")
    return coeffs
    
def quantize(coeffs: npt.NDArray[np.float64], qt: npt.NDArray[np.uint8]):
    """量子化テーブルに基づき各係数を除算し丸める
    
    Args:
        coeffs (npt.NDArray[np.float64]): DCT係数
        qt (npt.NDArray[np.uint8]): 量子化テーブル
        
    Returns:
        npt.NDArray[np.float64]: 量子化テーブルで除算し丸められたDCT係数
    """
    q_coeffs = np.round(coeffs / qt)
    return q_coeffs

def main():
    # 原画像をRGBで読み込む
    rgb_image = load_image("path/to/input")

    # RGBからYCbCrに変換する
    ycbcr = convert_color_space(rgb_image)

    # 色差信号を4:2:0で間引く
    y, cb, cr = chroma_sub_sampling(ycbcr)

    # qualityに応じて量子化テーブルをスケーリング
    quality = 75
    qp = 5000 / quality if quality < 50 else 200 - quality * 2.0
    luma_qt = np.floor((LUMINANCE_QUANTIZE_TABLE * qp + 50) / 100).clip(1, 255).astype(np.uint8)
    chroma_qt = np.floor((CHROMA_QUANTIZE_TABLE * qp + 50) / 100).clip(1, 255).astype(np.uint8)
    
    # 各チャンネルを8x8ブロックでDCTして量子化
    original_shape = ycbcr.shape[:2]
    channels = []
    for c, mode in zip((y, cb, cr), ("l", "c", "c")):
        qt = luma_qt if mode == "l" else chroma_qt
        coeffs = dct(c)
        q_coeffs = quantize(coeffs, qt)

if __name__ == "__main__":
    main()

量子化された8×8のDCT係数は、後段の符号化器によって(様々な情報を付与されて)符号化されます。この符号化されたデータがJPEGファイルとなります。
🎊おめでとうございます！JPEGエンコーダーにおけるDCT&量子化部分が完成しました。🎊

実験

　完成したDCTおよび量子化を使って、視覚特性を確かめる実験をしてみましょう。
例によってクリスマスツリーにイラストに対し、品質パラメーターを変えて量子化されたDCT係数を逆変換し、再構築した画像がこちらです。

qualityの値が小さくなるにつれて劣化が生じていることがわかるでしょうか。
また、色と色の境界において劣化が目立ち、品質が低い場合にはブロック状のノイズが確認できます。
このように、ブロック単位で処理をしている都合上イラストのような複数のベタ塗りで構成されるような画像では、高周波成分で発生した歪みが低周波領域に現れてしまうため劣化が目立ちやすく、JPEGの不得意な性質を持つ画像といえます。

　一方で、自然画像のようなカメラで撮影された画像に対しては、発生した劣化がそれほど目立たない場合が多いです。

おわりに

　おつかれさまでした。
ここまでの内容で、JPEGエンコーダーにおけるクロマサブサンプリング, DCT, 量子化部分と下記の情報を手に入れました。

  • デジタル画像には主にラスタ画像とベクタ画像があること
  • JPEGはラスタ画像の非可逆圧縮符号化方式であること
  • JPEGエンコーダーは人間の視覚特性を利用して画質をあまり落とさずに色差信号の情報量を削減していること
  • JPEGは画像を8×8ピクセルのブロックに分割して処理していること
  • DCTでは画像の空間的な冗長性を取り除き低周波成分にエネルギーを圧縮していること
  • JPEGエンコーダーは人間の視覚特性を利用して画質をあまり落とさずに高周波成分の情報量を削減していること


次回は、量子化されたDCT係数を短い符号列に圧縮するための符号化器(エンコーダー)について紹介したいと思います。
ここまでお付き合いいただきありがとうございました。次回もまたよろしくお願いします。

このページの先頭へ